子流形的共形几何和Willmore曲面
报告专家：王鹏（福建师范大学）
报告时间：7月13、20、27日,8月3日，14:30-17:00
报告地点：线上995-8498-1441
报告摘要：子流形的整体几何与拓扑是微分几何领域研究的核心研究方向之一, 其中一个代表性的问题为英国 数学家Willmore[61]在1965年提出的Willmore猜想:
S^{n} 中的任何一个二维环面都满足
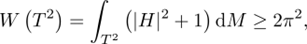
其中 H 为其平均曲率向量, 并且等号成立当且仅当此环面 (相差 S^{n} 的一个共形变换) 为Clifford环面.
关于Willmore泛函和其变分临界曲面的研究由来已久, 历史上最初见于 1816 年左右法国女数学家Germain关于弹性曲面能量的研究。1920年左右德国几何学家Blaschke及其学生Thompsen已经证明Willmore泛函是共形不变的, 并将其变分临界曲面-Willmore 曲面- 称为共形极小曲面, 并将其研究成果写入Blaschke关于微分几何的德语专著之中 [2]. 由于Willmore能量是共形不变的, 其研究自然成为共形微分几何研究中的核心问题之一, 吸引了全世界几何学家的研究目光。而在此问题的研究中, 数学家们发展了很多重要的研究工具并开创了多个新的研究方向.
本短期课程主要包含两部分，第一部分主要介绍子流形的共形几何，以及关于Willmore超曲面的广义Willmore猜想，第二部分主要介绍Willmore曲面和Willmore猜想的相关研究进展。
专家简介：王鹏，福建师范大学教授，闽江学者特聘教授。主要研究方向为Willmore曲面与极小曲面，主持国家自然科学基金面上项目2项，青年基金1项，在J. Differ. Geom., Adv.Math., Bull. London Math. Soc.等杂志上发表论文20余篇。
![[minicourse ]子流形的共形几何和willmore曲面--2-01.jpg](http://tianyuan.scu.edu.cn/upload/default/20220708/%5Bminicourse%20%5D%E5%AD%90%E6%B5%81%E5%BD%A2%E7%9A%84%E5%85%B1%E5%BD%A2%E5%87%A0%E4%BD%95%E5%92%8Cwillmore%E6%9B%B2%E9%9D%A2--2-01.jpg "[minicourse ]子流形的共形几何和willmore曲面--2-01.jpg")
VIDEOS