On the nonexistence of lattice tiling of Lee spheres
报告专家:周悦(国防科技大学)
报告时间:2024年7月23日(星期二)下午14:30-15:30
报告地点:数学学院西202报告厅
报告摘要:For any positive integers and , the Lee sphere of radius r centered at the origin in $\mathbb{Z}^n$ is defined by
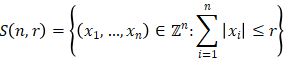
More than 50 years ago Golomb and Welch proved that the packing density of Lee spheres in $\mathbb{Z}^n$ tends to 0 as $n\rightarrow\infty$ provided that the radius of the Lee sphere is large enough compared with . In the same paper, they also conjectured that there is no perfect packing for r ≥ 2 and n ≥ 3. In particular, a perfect lattice packing of Lee spheres is equivalent to an abelian Cayley graph meeting the Moore-like bound. In this talk, I will summarize the known approaches for the Golomb-Welch conjecture and present some recent results using symmetric polynomials.
专家简介:周悦,国防科技大学数学系 研究员。主要研究有限几何、代数组合及其在编码密码中的应用,在Adv. Math., J. Cryptology, Combinatorica, JCTA等期刊发表论文50余篇。2016年获得国际组合及其应用学会Kirkman奖章,德国“洪堡”Fellow。2019年起担任国际期刊Designs, Codes and Cryptography编委。2021年获评国家级青年人才。
邀请人:连增 范久瑜

